Cara Uji Regresi Linier Berganda di SPSS

Regresi linier berganda merupakan salah satu teknik analisis statistik yang digunakan untuk menguji pengaruh lebih dari satu variabel independen terhadap satu variabel dependen. Metode ini banyak digunakan dalam berbagai bidang, seperti ekonomi, bisnis, sosial, dan sains, untuk memahami hubungan antara variabel serta membuat prediksi berdasarkan data yang ada.

Salah satu cara yang paling umum digunakan untuk melakukan uji regresi linier berganda adalah dengan menggunakan perangkat lunak SPSS (Statistical Package for the Social Sciences). SPSS memungkinkan pengguna untuk melakukan analisis regresi dengan mudah melalui fitur-fitur yang tersedia, seperti pengujian signifikansi model, uji asumsi klasik, serta interpretasi hasil regresi.

Dengan memahami cara uji regresi linier berganda di SPSS, pengguna dapat menganalisis hubungan antara variabel dengan lebih akurat dan membuat keputusan berdasarkan data yang tersedia. Materi ini akan membahas langkah-langkah rinci dalam melakukan uji regresi linier berganda di SPSS secara sistematis dan mudah dipahami.

Pengertian Uji Regresi Linier Berganda

Regresi linier berganda adalah metode analisis statistik yang digunakan untuk melihat pengaruh dua atau lebih variabel independen terhadap satu variabel dependen. Model ini merupakan pengembangan dari regresi linier sederhana yang hanya melibatkan satu variabel independen. Dengan adanya lebih dari satu variabel independen, analisis ini memungkinkan untuk mengeksplorasi hubungan yang lebih kompleks dan memberikan pemahaman yang lebih mendalam mengenai faktor-faktor yang memengaruhi variabel dependen.

Tujuan utama dari regresi linier berganda adalah untuk mengetahui sejauh mana variabel-variabel independen dapat menjelaskan variasi dalam variabel dependen, serta untuk menguji hubungan dan signifikansi pengaruh dari masing-masing variabel independen terhadap variabel dependen. Model ini sering digunakan dalam penelitian akademik maupun dunia bisnis untuk membantu dalam pengambilan keputusan berbasis data.

Dalam model regresi linier berganda, hubungan antar variabel dinyatakan dalam persamaan:

Y = b0 + b1X1 + b2X2 + ... + bnXn + e

Di mana:

• Y adalah variabel dependen (terikat) yang diprediksi berdasarkan variabel independen.
• X1, X2, ..., Xn adalah variabel independen (bebas) yang memengaruhi variabel dependen.
• b0 adalah konstanta (intersep) yang menunjukkan nilai Y saat semua variabel independen bernilai nol.
• b1, b2, ..., bn adalah koefisien regresi yang menunjukkan seberapa besar pengaruh masing-masing variabel independen terhadap variabel dependen.
• e adalah residual atau error dalam model, yang mewakili faktor-faktor yang tidak dapat dijelaskan oleh model regresi.

Dalam regresi linier berganda, asumsi yang harus dipenuhi mencakup linearitas hubungan antara variabel, tidak adanya multikolinearitas yang tinggi antara variabel independen, serta homoskedastisitas (variansi error yang konstan). Pelanggaran terhadap asumsi-asumsi ini dapat menyebabkan hasil analisis menjadi tidak valid atau bias.

Salah satu cara yang paling umum digunakan untuk melakukan uji regresi linier berganda adalah dengan menggunakan perangkat lunak SPSS (Statistical Package for the Social Sciences). SPSS memungkinkan pengguna untuk melakukan analisis regresi dengan mudah melalui fitur-fitur yang tersedia, seperti pengujian signifikansi model, uji asumsi klasik, serta interpretasi hasil regresi. SPSS juga menyediakan berbagai alat bantu visualisasi yang mempermudah analisis dan pemahaman terhadap hubungan antar variabel.

Analisis regresi linier berganda dalam SPSS melibatkan beberapa langkah penting, yaitu:

• Menyiapkan dan memasukkan data ke dalam SPSS – Pastikan data telah dikodekan dengan benar dan variabel telah didefinisikan sesuai jenisnya.
• Melakukan uji asumsi klasik – Uji ini mencakup pengujian normalitas residual (untuk memastikan bahwa error terdistribusi normal), uji multikolinearitas (untuk memastikan tidak ada korelasi tinggi antar variabel independen), uji heteroskedastisitas (untuk memastikan variansi error konstan), dan uji autokorelasi (terutama dalam data runtun waktu).
• Melakukan analisis regresi linier berganda – Menjalankan perintah regresi di SPSS untuk mendapatkan hasil analisis koefisien regresi, nilai R-squared, dan signifikansi model.
• Menginterpretasikan hasil analisis – Ini mencakup interpretasi terhadap nilai koefisien regresi, uji signifikansi (p-value), serta koefisien determinasi (R²) yang menunjukkan sejauh mana variabel independen mampu menjelaskan variasi dalam variabel dependen.
• Menarik kesimpulan dan membuat rekomendasi – Berdasarkan hasil analisis, pengguna dapat menentukan variabel mana yang memiliki pengaruh signifikan serta membuat rekomendasi berdasarkan hasil regresi.

Dengan memahami cara uji regresi linier berganda di SPSS, pengguna dapat menganalisis hubungan antara variabel dengan lebih akurat dan membuat keputusan berdasarkan data yang tersedia. Materi ini akan membahas langkah-langkah rinci dalam melakukan uji regresi linier berganda di SPSS secara sistematis dan mudah dipahami. Selain itu, akan dijelaskan bagaimana mengatasi kemungkinan pelanggaran asumsi serta strategi dalam meningkatkan validitas model regresi yang digunakan. Dengan pemahaman yang baik mengenai regresi linier berganda, pengguna dapat mengoptimalkan analisis statistik dalam berbagai bidang penelitian dan aplikasi praktis.

Syarat Data Uji Regresi Linier Berganda

Sebelum melakukan analisis regresi linier berganda, terdapat beberapa syarat yang harus dipenuhi agar hasil analisis valid, akurat, dan dapat diinterpretasikan dengan baik. Syarat-syarat tersebut mencakup aspek asumsi dasar regresi yang harus diperhatikan dalam setiap analisis statistik untuk memastikan model yang digunakan dapat menggambarkan hubungan antara variabel dengan baik.

Hubungan Linier

Salah satu asumsi utama dalam regresi linier berganda adalah bahwa hubungan antara variabel dependen dan variabel independen harus bersifat linier. Jika hubungan antara variabel tidak linier, maka model regresi yang digunakan akan memberikan hasil yang bias dan tidak valid.

Selain scatter plot, uji linearitas juga dapat dilakukan menggunakan metode statistik seperti uji Ramsey RESET di SPSS, yang dapat mengidentifikasi apakah terdapat hubungan non-linier dalam model regresi.

Tidak Ada Multikolinearitas

Multikolinearitas terjadi ketika dua atau lebih variabel independen dalam model memiliki korelasi yang tinggi satu sama lain. Hal ini dapat menyebabkan ketidakstabilan dalam estimasi koefisien regresi dan membuat interpretasi hasil menjadi sulit.

Untuk mengatasi multikolinearitas, salah satu solusinya adalah dengan menghapus salah satu variabel independen yang memiliki korelasi tinggi atau melakukan teknik seperti Principal Component Analysis (PCA) untuk mengurangi dimensi data.

Residual Berdistribusi Normal

Residual dalam model regresi harus berdistribusi normal agar hasil estimasi parameter regresi dapat digunakan untuk inferensi statistik yang valid.

Jika residual tidak berdistribusi normal, maka dapat dilakukan transformasi data seperti logaritma natural (Ln) atau Box-Cox transformation untuk memperbaiki normalitas data.

Homoskedastisitas

Homoskedastisitas mengacu pada asumsi bahwa variansi residual tetap konstan di seluruh rentang variabel independen. Jika asumsi ini dilanggar, maka model regresi mengalami heteroskedastisitas, yang dapat menyebabkan kesalahan dalam estimasi parameter.

Jika ditemukan heteroskedastisitas, solusi yang dapat dilakukan adalah dengan menggunakan transformasi variabel, seperti mengambil akar atau logaritma dari variabel dependen, atau menggunakan metode regresi yang lebih robust seperti regresi weighted least squares (WLS).

Tidak Ada Autokorelasi

Autokorelasi terjadi ketika residual memiliki pola tertentu yang berulang dari waktu ke waktu, yang umum ditemukan dalam data runtun waktu (time series). Autokorelasi menyebabkan hasil regresi tidak valid karena melanggar asumsi independensi residual.

Jika ditemukan autokorelasi, metode yang dapat digunakan untuk mengatasinya adalah menambahkan lag variabel dalam model regresi atau menggunakan autoregressive models (AR).

Variabel Independen Harus Relevan

Variabel independen yang digunakan dalam model harus memiliki relevansi yang jelas dengan variabel dependen untuk menghindari bias dalam hasil regresi.

Pemilihan variabel independen dapat dilakukan dengan:

• Uji signifikansi koefisien regresi untuk memastikan bahwa variabel independen yang digunakan memiliki pengaruh yang signifikan terhadap variabel dependen.
• Stepwise regression atau Backward elimination untuk menyaring variabel independen yang kurang signifikan.
• Menggunakan teori dan penelitian sebelumnya sebagai dasar pemilihan variabel independen yang relevan.
• Jika terdapat variabel independen yang tidak relevan dalam model, maka hasil regresi bisa menjadi bias dan kurang akurat dalam memprediksi variabel dependen.

Dengan memenuhi semua syarat di atas, analisis regresi linier berganda dapat menghasilkan model yang valid dan akurat. Hal ini sangat penting dalam penelitian dan pengambilan keputusan berbasis data karena model regresi yang baik dapat memberikan wawasan yang lebih dalam terhadap hubungan antar variabel serta meminimalisir kesalahan dalam interpretasi hasil. Jika salah satu dari syarat ini tidak terpenuhi, maka langkah-langkah perbaikan perlu dilakukan agar hasil regresi tetap dapat digunakan dengan baik dalam analisis statistik.

Cara Uji Regresi Linier berganda di SPSS

Berikut adalah langkah-langkah untuk melakukan Uji Regresi Linier Berganda di SPSS setelah melakukan uji asumsi klasik

Membuka Menu Regresi Linier

Klik Analyze → Regression → Linear.

Memasukkan Variabel

Masukkan variabel dependen (Y) ke dalam kotak Dependent.

Masukkan variabel independen (X1, X2, X3, dst.) ke dalam kotak Independent(s).

Mengatur Statistik Tambahan (Opsional)

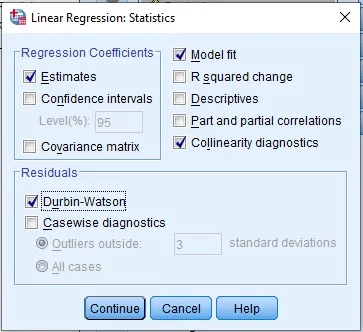
Klik Statistics, lalu centang opsi berikut sesuai kebutuhan:

• Estimates (untuk menampilkan koefisien regresi)
• Model Fit (untuk menampilkan nilai R²)
• Collinearity Diagnostics (untuk memeriksa multikolinearitas)
• Durbin-Watson (untuk memeriksa autokorelasi)

Klik Continue untuk kembali ke menu utama. dan OK untuk menjalankan analisis regresi.

SPSS akan menampilkan hasil analisis dalam output.

Cara Membaca Hasil Uji Regrersi Linier Berganda

Berikut adalah cara membaca hasil Uji Regresi Linier Berganda di SPSS beserta interpretasinya

• Tabel Model Summary

• Tabel Model Summary dalam output SPSS memberikan informasi tentang kualitas model regresi dalam menjelaskan hubungan antara variabel independen dan variabel dependen.

R (Koefisien Korelasi)

Nilai R menunjukkan hubungan antara variabel independen dan variabel dependen.

• Interpretasi nilai R
• • 0,00 – 0,19 → Hubungan sangat lemah
  • 0,20 – 0,39 → Hubungan lemah
  • 0,40 – 0,59 → Hubungan sedang
  • 0,60 – 0,79 → Hubungan kuat
  • 0,80 – 1,00 → Hubungan sangat kuat

Nilai R menunjukkan tingkat hubungan antara variabel independen (Harga Produk, Biaya Iklan, dan Jumlah Sales) terhadap variabel dependen (Penjualan).

Nilai R 0.105 menunjukkan hubungan yang sangat lemah antara faktor-faktor tersebut terhadap penjualan.

R Square (R² / Koefisien Determinasi)

R Square menunjukkan seberapa besar variabel independen mampu menjelaskan variasi dalam variabel dependen.

R Square merupakan variasi dalam variabel dependen dapat dijelaskan oleh variabel independen yang digunakan dalam model regresi, Sisanya dipengaruhi oleh faktor lain yang tidak dimasukkan dalam model.

Semakin tinggi R², semakin baik model dalam menjelaskan hubungan antara variabel.

Jika selisih antara R² dan Adjusted R² kecil, berarti variabel dalam model sudah tepat dan tidak ada variabel yang tidak perlu.

Hanya 1.1% variasi dalam Penjualan dapat dijelaskan oleh Harga Produk, Biaya Iklan, dan Jumlah Sales.

Sisanya (98.9%) dijelaskan oleh faktor lain yang tidak dimasukkan dalam model.

Std. Error of the Estimate (Kesalahan Standar Estimasi)

Std. Error of the Estimate menunjukkan besarnya kesalahan dalam memprediksi variabel dependen.

Semakin kecil nilai ini, semakin akurat model dalam memprediksi variabel dependen.

Ini adalah standar error dari model, menunjukkan seberapa jauh prediksi dari nilai aktual Penjualan.

Nilai Std. Error of the Estimate = 161,970,911.327 yang besar menunjukkan bahwa model memiliki tingkat kesalahan prediksi yang cukup tinggi.

• Tabel ANOVA (Uji F)

• Tabel ANOVA dalam output regresi linear berganda di SPSS digunakan untuk menguji signifikansi keseluruhan model regresi dengan Uji F.

• Tabel ANOVA digunakan untuk menguji signifikansi keseluruhan model regresi, yaitu apakah variabel independen (Harga Produk, Biaya Iklan, dan Jumlah Sales) secara bersama-sama berpengaruh signifikan terhadap variabel dependen (Penjualan).

Sum of Squares (Jumlah Kuadrat)

Rumus hubungan antar nilai

Total Sum of Squares = Regression Sum of Squares + Residual Sum of Squares

• Regression → menunjukkan variasi dalam variabel dependen yang dapat dijelaskan oleh model regresi (variabel independen).
• Residual  → menunjukkan variasi dalam variabel dependen yang tidak dapat dijelaskan oleh model (kesalahan).
• Total → total variasi dalam variabel dependen.

Semakin besar Regression Sum of Squares dibandingkan Residual Sum of Squares, semakin baik model dalam menjelaskan variabel dependen.

Mean Square (Rata-rata Kuadrat)

• Mean Square Regression → diperoleh dari Sum of Squares Regression / df Regression
• Mean Square Residual → diperoleh dari Sum of Squares Residual / df Residual

df (Derajat Kebebasan) df1 = 3 dan df2 = 96

• Regression df → jumlah variabel independen dalam model.
• Residual df → jumlah total sampel dikurangi jumlah variabel independen + 1 (df = n - k - 1).
• Total df → jumlah total observasi dikurangi 1 (df = n - 1).
• df1 (derajat bebas regression) = 3 (jumlah variabel independen)
• df2 (derajat bebas residual) n - k = 96 = 96 (jumlah sampel - jumlah parameter)
• Dengan α = 0.05, cari nilai F tabel(df1=3, df2=96) di tabel distribusi F sebesar 2,70

Menentukan Nilai F-Tabel 2,7

Mencari F-tabel dari Tabel Distribusi F

Tingkat signifikansi (α) = 0.05

F-Statistic (Uji F)

Uji F digunakan untuk menilai apakah model regresi secara keseluruhan signifikan dalam menjelaskan variasi variabel dependen (Penjualan).

• F = Mean Square Regression / Mean Square Residual
• • Nilai F yang tinggi menunjukkan bahwa model secara keseluruhan signifikan, artinya variabel independen secara bersama-sama mempengaruhi variabel dependen.
  • Nilai F yang rendah menunjukkan bahwa model secara keseluruhan tidak signifikan, artinya variabel independen secara bersama-sama kurang mempengaruhi variabel dependen.

Untuk menentukan apakah model signifikan, bandingkan F-hitung dengan F-tabel.

• Hipotesis Uji F
• • H0 (Hipotesis Nol): Model regresi tidak signifikan, atau variabel independen secara bersama-sama tidak tidak berpengaruh signifikan terhadap Penjualan.
  • H1 (Hipotesis Alternatif): Model regresi signifikan, atau variabel independen secara bersama-sama berpengaruh signifikan terhadap Penjualan.

• Kriteria Pengambilan Keputusan
• • Jika F hitung > F tabel, maka H0 ditolak,  model regresi signifikan secara statistik layak digunakan untuk analisis lebih lanjut (model signifikan).
  • Jika F hitung ≤ F tabel, maka gagal menolak H0, model regresi tidak signifikan secara statistik dan perlu direvisi atau mencari variabel lain yang lebih relevan (model tidak signifikan).

• Perbandingan F Hitung vs F Tabel

• Bandingkan nilai F hitung dengan F tabel pada tingkat signifikansi α = 0.05.

  F hitung = 0.358 (dari tabel ANOVA)

  F tabel = 2.70

  Karena F hitung (0.358) < F tabel (2.70), maka gagal menolak H0.

• Kesimpulan Uji F
• • Model regresi secara keseluruhan tidak signifikan dalam menjelaskan Penjualan.
  • Variabel Harga Produk, Biaya Iklan, dan Jumlah Sales secara bersama-sama tidak berpengaruh signifikan terhadap Penjualan.
  • Model ini tidak cocok dan perlu direvisi, misalnya dengan menambahkan variabel lain yang lebih relevan.

Sig. (p-value)

Nilai Signifikansi (Sig.)

Pada tabel ANOVA, nilai Sig. yang diberikan adalah 0.784.

Nilai ini menunjukkan probabilitas bahwa hasil regresi terjadi secara kebetulan.

• Batas Signifikansi (Alpha = 0.05)

• Dalam analisis regresi, digunakan batas signifikansi 0.05 (atau 5%).

  • Jika Sig. < 0.05, maka model regresi secara keseluruhan signifikan dan dapat digunakan untuk memprediksi variabel dependen.
  • Jika Sig. ≥ 0.05, maka model tidak signifikan, artinya variabel independen secara bersama-sama tidak memiliki pengaruh yang signifikan terhadap variabel dependen.

• Interpretasi Hasil

• Karena Sig. = 0.784 (lebih besar dari 0.05), maka model regresi tidak signifikan secara statistik.

  Artinya, kombinasi variabel Jumlah Sales, Biaya Iklan, dan Harga Produk tidak cukup kuat dalam menjelaskan variasi variabel Penjualan.

  Dengan kata lain, kemungkinan besar variabel independen ini tidak memiliki pengaruh yang cukup berarti terhadap variabel dependen atau ada faktor lain yang lebih dominan dalam mempengaruhi Penjualan.

• Tabel Coefficients (Uji t)

• Tabel Coefficients dalam output regresi linier berganda di SPSS digunakan untuk menguji pengaruh masing-masing variabel independen terhadap variabel dependen secara parsial dengan Uji t. Tabel Coefficients digunakan untuk menguji pengaruh masing-masing variabel independen secara individual terhadap variabel dependen (Penjualan) dengan menggunakan Uji t.

  Model regresi yang terbentuk

  Y = 341629108,9 + 3409,199 X1 Harga Produk − 6,167 X2 Biaya Iklan - 234976,174 X3 Jumlah Sales

Unstandardized Coefficients (B)

Kolom B menunjukkan besarnya pengaruh masing-masing variabel independen terhadap variabel dependen dalam satuan asli.

• Intercept (Constant) = 341,629,108.860

• Jika semua variabel independen bernilai nol, maka nilai Penjualan sebesar 341,629,108.86.

• Harga Produk (B = 3,409.188)

• Jika Harga Produk naik 1 satuan, maka Penjualan naik sebesar 3,409.19, dengan asumsi variabel lainnya tetap.

• Biaya Iklan (B = -6.167)

• Jika Biaya Iklan naik 1 satuan, maka Penjualan turun sebesar 6.167, dengan asumsi variabel lainnya tetap.

• Jumlah Sales (B = -234,976.174)

• Jika Jumlah Sales naik 1 satuan, maka Penjualan turun sebesar 234,976.174, dengan asumsi variabel lainnya tetap.

• uji signifikansi
• • Jika nilai B positif, berarti variabel tersebut memiliki pengaruh positif terhadap variabel dependen.
  • Jika nilai B negatif, berarti variabel tersebut memiliki pengaruh negatif terhadap variabel dependen.

Unstandardized Coefficients (Std. Error)

Unstandardized Coefficients Std. Error menunjukkan tingkat ketidakpastian (variabilitas) dari estimasi koefisien regresi (B).

Semakin kecil nilai Std. Error, semakin stabil dan akurat estimasi koefisien B.

sementara semakin besar nilai Std. Error, semakin tinggi ketidakpastian dalam prediksi model.

Standardized Coefficients (Beta)

Standardized Coefficients (Beta) digunakan untuk mengukur seberapa besar pengaruh masing-masing variabel independen terhadap variabel dependen dalam skala yang sama. Berbeda dengan Unstandardized Coefficients (B) yang menggunakan satuan asli data, nilai Beta telah dinormalisasi sehingga bisa dibandingkan langsung antar variabel.

Semakin besar nilai Beta (baik positif maupun negatif), semakin kuat pengaruh variabel tersebut terhadap variabel dependen (Penjualan). Jika nilai Beta mendekati 0, berarti pengaruh variabel tersebut sangat kecil atau tidak signifikan.

t-Statistic (Uji t)

Kolom t menunjukkan hasil Uji t, yang digunakan untuk menguji apakah setiap variabel independen memiliki pengaruh yang signifikan terhadap variabel dependen secara individual.

Nilai t dalam tabel Coefficients digunakan untuk menguji apakah masing-masing variabel independen memiliki pengaruh yang signifikan terhadap variabel dependen (Penjualan). 

Nilai t diperoleh dari perhitungan : t = B / Std.error

Semakin besar nilai t (baik positif maupun negatif), semakin besar variabel tersebut memiliki pengaruh signifikan terhadap variabel dependen.

• Menentukan Nilai t Tabel

• Nilai t tabel dihitung berdasarkan

  Tingkat signifikansi (α) = 0.05 (dua arah)

  Derajat kebebasan (df) = n - k - 1

  n = jumlah sampel = 100

  k = jumlah variabel independen = 3

  df = 100 - 3 - 1 = 96

  Dari tabel distribusi t, diperoleh t tabel = 1.985 (untuk df = 96 dan α = 0.05).

• Hipotesis Uji t

• H0 (Hipotesis Nol): Variabel independen tidak berpengaruh signifikan terhadap variabel dependen (Penjualan).

  H1 (Hipotesis Alternatif): Variabel independen berpengaruh signifikan terhadap variabel dependen (Penjualan).

• Interprestasi Perbandingan t Hitung dengan t Tabel

• Konstanta t Hitung 1.339 < t Tabel 1.985 Gagal menolak H0 (Tidak signifikan)

  Konstanta tidak signifikan dalam model, yang berarti ketika semua variabel independen bernilai nol, prediksi Penjualan oleh model tidak cukup akurat.

  Harga Produk t hitung 0.124 < t Tabel 1.985 Gagal menolak H0 (Tidak signifikan)

  Harga Produk tidak berpengaruh signifikan terhadap Penjualan. Perubahan harga produk tidak memiliki dampak signifikan terhadap jumlah penjualan.

  Biaya Iklan t hitung -1.032 < t Tabel 1.985 Gagal menolak H0 (Tidak signifikan)

  Biaya Iklan tidak signifikan terhadap Penjualan. Meskipun ada hubungan negatif antara biaya iklan dan penjualan, hubungan ini tidak cukup kuat secara statistik.

  Jumlah Sales t hitung -0.044 < t Tabel 1.985 Gagal menolak H0 (Tidak signifikan)

  Jumlah tenaga sales tidak signifikan terhadap Penjualan. Peningkatan jumlah sales tidak secara langsung berdampak pada peningkatan penjualan.

• Kesimpulan Akhir Uji t

• Semua variabel memiliki t hitung yang lebih kecil dari t tabel, sehingga tidak ada variabel independen yang memiliki pengaruh signifikan terhadap Penjualan.

  Model regresi ini tidak cukup kuat untuk menjelaskan hubungan antara vari

Sig. (p-value)

Kolom Sig. (p-value) menunjukkan tingkat signifikansi masing-masing variabel independen.

Jika nilai t kecil, maka pengaruhnya terhadap variabel dependen lemah atau tidak signifikan.

Semakin besar nilai t, semakin kuat bukti bahwa variabel independen berpengaruh terhadap variabel dependen

• Hipotesis Uji t

• H0: Variabel tidak berpengaruh terhadap Penjualan.

  H1: Variabel berpengaruh terhadap Penjualan.

• Kriteria Pengambilan Keputusan

• Jika Sig. < 0.05, maka tolak H0 (variabel berpengaruh signifikan terhadap penjualan).

  Jika Sig. > 0.05, maka gagal tolak H0 (variabel tidak berpengaruh signifikan terhadap penjualan).

• Hasil Uji t

• Harga Produk (Sig. = 0.902)  > 0.05 → tidak signifikan

  Biaya Iklan (Sig. = 0.305) > 0.05 → tidak signifikan

  Jumlah Sales (Sig. = 0.965) > 0.05 → tidak signifikan

• Kesimpulan Uji t

• Semua variabel memiliki nilai Sig. > 0.05, Sehingga Tidak ada variabel independen yang berpengaruh signifikan terhadap Penjualan (Harga Produk, Biaya Iklan, dan Jumlah Sales semuanya tidak signifikan).

  Model ini tidak baik dalam menjelaskan variabel Penjualan, sehingga perlu perbaikan, misalnya dengan menambahkan variabel lain yang lebih relevan.

  Perlu dilakukan eksplorasi lebih lanjut, seperti menambahkan variabel lain atau menggunakan model regresi yang lebih kompleks.